The current standard for floating point arithmetic has no means of measuring and/or recording floating point error introduced because of the inability to represent real numbers in a finite space.
The object of this invention is to bound floating point error when performing floating point arithmetic operations in a floating point processing device.
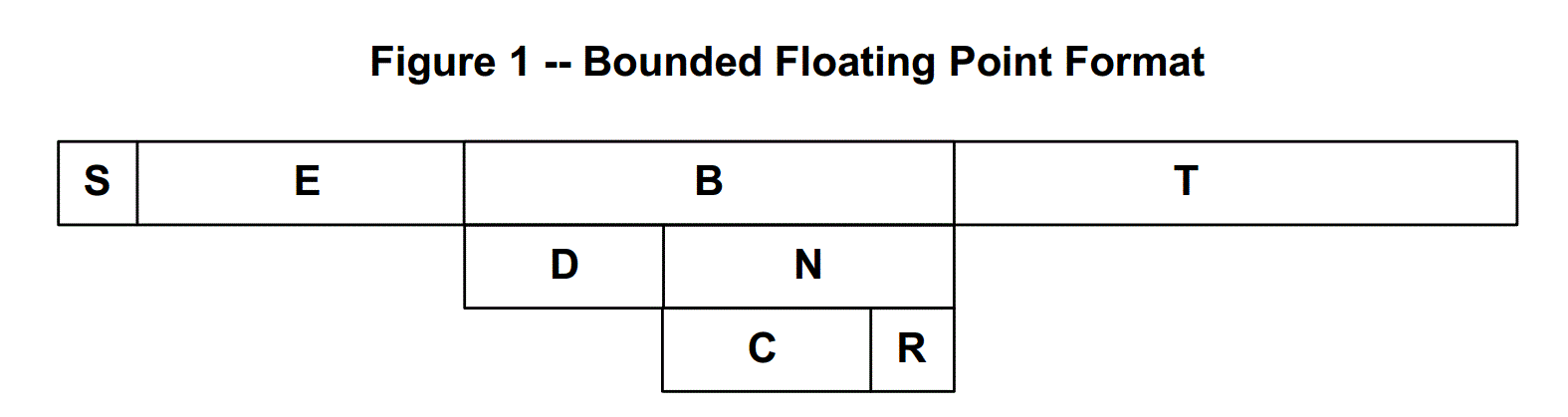
This invention provides a device that performs floating point operations while calculating and retaining a bound on floating point error. This is accomplished by inserting an additional field, the bound field, B, into the ANSI/IEEE 754-2008 standard floating point arithmetic format. This new bound field supplements the conventional floating point standard to provide accumulated information for the bound of the error that delimits the real number represented.
Figure 1 shows the organization of the bit fields in the representation of bounded floating point numbers. Field widths vary depending on the "precision" (the total width of the representation).

The bound field has two major parts, the lost bits field,D, and the accumulated rounding error field,N. The N field is subsequently divided into the rounding bits field, R, and the rounding error count field, C.
Basically, the lost bits field is the logarithm of the error bound of the floating point number. The lost bits field is the number of bits in the floating point representation that are no longer significant. This invention provides a device for computing the value of D during floating point operations.
D is affected directly by cancellation error from normalization during subtraction, and other operations.
The accommodation of rounding error, however, provides a more difficult problem. The rounding error count field, C, is the accumulation of rounding errors. When the log of C exceeds the value of D, D is incremented and C is reset. However, when the value is C is such that the log of C exceeds the maximum value that can be contained in C, then D is incremented and C is reset.
The R field is the sum of the most significant bits of an operation that are lost by truncation of the result. R is also incremented by the equivalent of a "sticky bit", the presence of one or more additional bits that are lost during shifting or truncation, thus providing an upper bound on the rounding error. The sum of the R Fields of subsequent operations carries into the C field.
Figure 2 shows the organization of the bit fields in the representation of normalized results of an operation. The field widths are associated with the field widths of Figure 1.

The H field is the hidden bit which does not appear in the result. The T field of the Post Normalization Result becomes the T field of the result in Figure 1. R is the most significant bits that are lost due to truncation and when any bit appears in X (or is shifted off the right) one is added to the value of R that will be added to the R field of Figure 1 for the result. Carries out of the R field addition in Figure 1 are added to the C field.
As a consequence, for normalized bounded floating point values, the represented real value lies between:
-1S · ((T+2t)/2t-1)E-O and -1S · ((T+2t+2D)/2t-1)E-O
(where t is the width of the significand and O is the exponent offset), and for denormalized values (where the E field is zero and there are no hidden bits), the first and second bounds of the represented real value are the following:
-1S · T/2t-1 and -1S · (T+2D)/2t-1
The average of the first and second bounds is an approximation of the expected value.
Representation of the Bound of Floating Point Error
In contrast to the conventional floating point standard that does not retain error information within the associated floating point data structure, this invention provides error information in the lost bits D Field within the floating point data structure. Two bounds are provided. Although using current technology error can be reduced by increasing computation time and/or memory space, the present invention provides this error information within the present data structure with little impact on space and performance.
The bounds on the real value represented are determined from the truncated floating point value (lower bound) and the addition of the error to the lower bound (upper bound). The upper bound is computed by the floating point number computed by adding the number of lost bits, D, to the exponent of the lower bound.
This invention can be used in conjunction with the concurrently with implementions of the current floating point standard. Conversion between this new format (BFP) and the current format can be accomplished when needed and therefore existing software that is dependent upon the current floating point standard need not be discarded.
This invention provides error notification by comparing the lost bits,D, to the (optionally programmable) acceptable loss of significance to provide a fail-safe, programmable real-time notification of the loss of significant bits, sNAN. This is in contrast to the current technology, which does not provide an indication when the result of a computation no longer provides a sufficient number of significant bits. This option would be applied at the final computation of a series of computations if desired. The value of D is not allowed to exceed the size of the significand (plus one for the hidden bit) and thus may indicate that the result has no significant bits.
This is an advantage over the current technology that does not permit any control on the allowable error. This invention, not only permits the detection of loss of significant bits, but also allows the number of required retained significant digits to be specified. When the loss of significant bits is greater than the acceptable limit, this circuit optionally generates a new signaling NaN (“sNaN)”) indicating that the result no longer has the required number of significant digits.
In the standard floating point implementation cancellation injects significant error without a corresponding indication in the result. In contrast, this invention accounts for cancellation error in the lost bits D Field.
Conversion from external to internal format (or between internal formats) may inject an error in the representation of a real number without recording that error. This invention provides a device for recording the error injected by the conversion of an external representation to the BFP internal representation (or of recording the error in conversion between internal representations).
At present standard floating point values are converted to external representation without indication of loss of significant digits even when no significant bits exist. In contrast, this invention allows for the display of only the significant decimal digits or optionally provides sNaN when insufficient significant bits remain.